Chyba wiem czemu widzę Gdynie z Juraty ;-)

Będąc w Juracie widuję Gdynię i stojący tam Sea Towers.

No i jest problem ;-) 

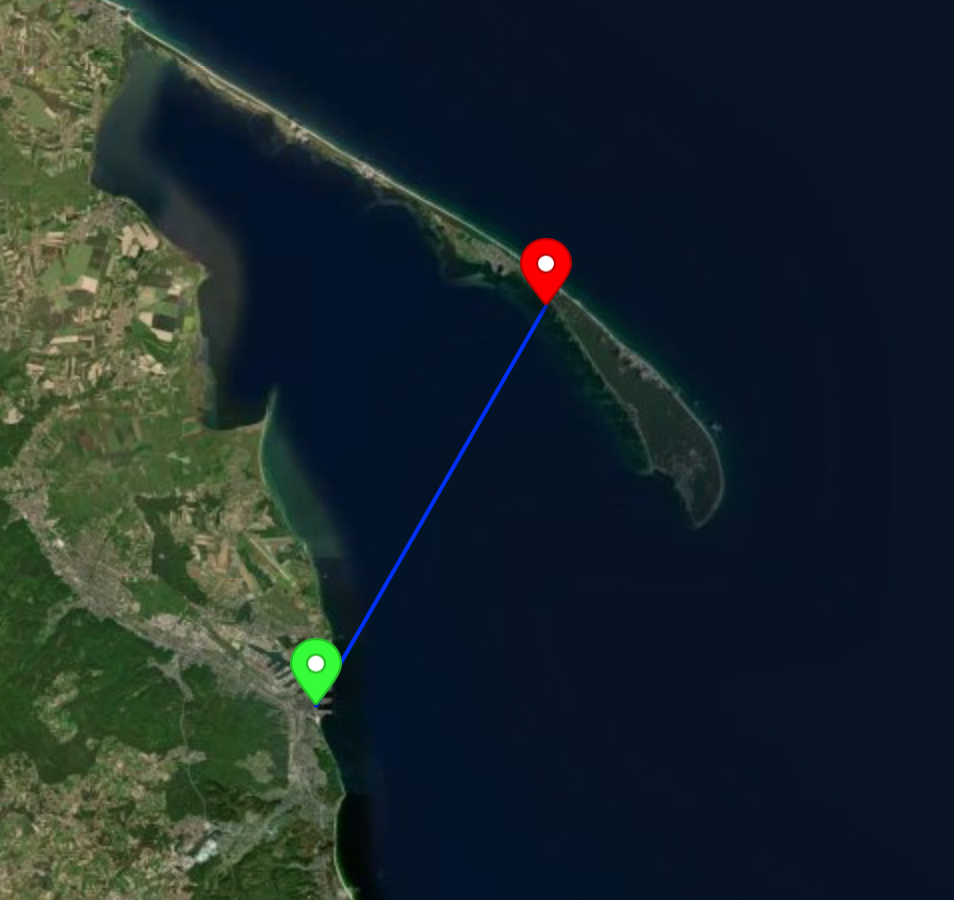
Horyzont powinien być jakieś 4.7-8* km ode mnie, a Sea Towers w Gdyni jest 20.35 km od czubka mola w Juracie (wg Google Maps). 

Czerwone to czubek mola w Juracie, zielone to Sea Towers w Gdyni, a niebieskie to tak koło 20 km odległości ;-)

(tutaj link do tego ;-))

Jak więc mogę widzieć Gdynię?

Gdy tam byłem w latach 80 to nie zawsze było widać Gdynię i ogólnie mówiono, że to jest Fata Morgana.

No i teoretycznie mogłaby być, bo morze jest chłodniejsze zwykle od powietrza (w lato przynajmniej) i chłodzi powietrze nad sobą i wtedy światło zakrzywia się tak, że "sięga za horyzont". 

Ale tam czasem nawet widać Gdańsk i żurawie portu północnego, a to już ponad 30 km....

I tak się zastanawiałem i chyba wiem ;-)

Skoro ja z 1.84 m wzrostu widzę na jakieś 4.7 km, to znaczy, że jeśli coś jest 9.4 km ode mnie w linii prostej i oddziela nas jedynie horyzont to jak to coś jest wyższe niż ja to mogę to widzieć.... przynajmniej tą część która wystaje ;-)

Skoro Sea Towers jest 20.35 km ode mnie to tak pi razy oko widzieć powinienem najmniej wszystko z niej powyżej jakichś 18.5 jej wysokości ;-)

A, że tak naprawdę mój punkt obserwacji to tak naprawdę z 5 metrów (molo jest wyżej niż brzeg nad zatoką o jakieś 1.5 metra, a sam poziom wody jest też z jakieś 1.5-1.7 niżej) to powinienem widzieć wszytko wyższe niż jakieś 11.5 metra w Gdyni ;-) a że sam budynek tak lekko licząc jest jakieś 6-10 metrów nad poziomem wody... to całe 142 metry wysokości powinienem widzieć ;-)

To samo z portem północnym... chociaż tu by musiały mieć żurawie ponad 37 metrów by widzieć ich czubki, a widać duży ich kawałek... i nie zawsze je widać, stąd tutaj dodałbym jednak jeszcze Fata Morganę ;-)

Ale teraz mi się powoli fizyka zaczyna zgadzać :-)

* - Horyzont jest w odległości liczonej wg wzoru:

hDist = Math.sqrt((h+R)^2-R^2), gdzie R = 6378.137 km

Czyli przy moim wzroście powinienem widzieć mniej więcej na 4.7 km, podobnie wyjdzie z wzoru przybliżonego:

hDist = sqrt(13*h)

gdzie h jest w metrach, a hDist w km, wtedy mamy ~4.8 km, skąd mi wyszło 8 km? Z tego, że jednak molo ma swoją wysokość nad poziomem morza, dałem mu kila metrów "wysokości"

Podobne posty^beta
Duża daleka góra
Tam gdzieś jest foka...
Jak się profesjonalnie kłamie
Książkowy listopad
Takie tam przemyślenia i refleksje ;-)